¿Donde se utiliza?
Las funciones cuadráticas son utilizadas en algunas disciplinas como, por ejemplo, Física y Economía.
En arquitectura es frecuente emplear arcos de parábola en distintas construcciones , por ejemplo en techos de tinglados , en arcos construidos en la avenida de entrada de un pueblo o ciudad o en puentes peatonal, como el construido sobre Av José I. de la Roza en la ciudad de San Juan.
También se puede ver en el recorrido del botar de una pelota de tenis o la trayectoria que describe el chorro de agua lanzado hacia arriba en la fuente de una plaza.

Definición:
Es toda función cuya fórmula es de la forma f(x) = ax2+bx+c , donde a, b y c son números reales, y a≠0.
El gráfico de una función cuadrática en el plano cartesiano es una curva llamada parábola.
Es una función polinómica de segundo grado, ya que ningún termino tiene un grado mayor que dos.
Los términos de una función cuadrática son:
La función cuadrática puede ser expresada de distintas formas.
Gráfica de la parábola
Para realizar el gráfico de una parábola , f(x) = ax2+bx+c , se deben calcular los elementos de la misma y luego representarla.
Raíces de la parábola.
Son los puntos de intersección de la parábola con el eje x. Es decir, cuando f(x)=0.
Para su cálculo se utiliza la fórmula de Baskara:
Mediante la fórmula se obtienen los valores de x1 y x2.
La gráfica puede cortar al eje x en dos puntos, en un solo punto o puede no cortarla.
El Discriminante.
Si observamos la fórmula que permite calcular las raíces de una función cuadrática resolviendo la ecuación ax2+bx+c=0 :
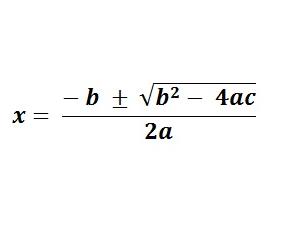
hay una operación , la raíz cuadrada, que presenta distintas posibilidades:
- Si b2-4ac
> 0 » tenemos dos soluciones posibles.
- Si b2-4ac = 0 » el resultado de la raíz cuadrada será 0, con lo cual la ecuación tiene una única solución.
- Si b2-4ac < 0 » entonces la raíz cuadrada no puede resolverse, con lo cual la ecuación no tendrá solución en el conjunto de los números reales.

El Discriminante se denota con la letra griega mayúscula delta:∆.
Es la expresión bajo el signo de la raíz cuadrada en la fórmula Resolvente de Baskara.
En definitiva, el Discriminante permite anticipar si la parábola cortará el eje x en dos puntos , en uno o en ninguno.

Función Cuadrática y Ecuación Cuadrática
Es importante no confundirlas.
La función cuadrática tiene la forma f(x)=ax2+bx+c (con a≠0).
A cada valor de x le corresponde un único valor de y. Su gráfica es una parábola.
En cambio, ax2+bx+c = 0 es una ecuación cuadrática.Sus soluciones reales, cuando las tiene, brindan las raíces de la función cuadrática, o sea, dan las abscisas para las cuales la función cuadrática en cero.
Eje de simetría
Es la recta paralela al eje y , que divide la curva en dos ramas simétricas,
Se puede hallar su ecuación empleando la fórmula:

Vértice
Es el punto del eje de simetría en el que la función pasa de decreciente a creciente , o viceversa.Por lo tanto, la ordenada del vértice , yv, es el mínimo (o el máximo) de la función.
Abertura o Concavidad
Si a > 0, la parábola es abierta hacia arriba ; si a < 0 , es abierta hacia abajo.
Coeficiente principal (a)
Cuanto mayor sea │a│, mas cerradas estarán las ramas, o dicho de otra forma, la parábola será mas estilizada.
Ordenada al origen
La ordenada al origen , f(0) es la ordenada del punto de intersección entre la parábola y el eje de ordenadas , o sea, es el valor que toma y cuando x = 0.
Si la función esta expresada en forma polinómica , la ordenada al origen es igual al termino independiente.
Dominio
Es el conjunto formado por todos los valores de la variable independiente (x) cuya imagen está definida según la función F(x).
Imagen
Es el conjunto formado por todos los valores de la variable dependiente (y) que tienen como pre imagen al menos un valor correspondiente al Dominio de la Función.
Crecimiento y Decrecimiento
El eje de simetría marca el crecimiento o decrecimiento de una función.
La función es positiva cuando se encuentra arriba del eje x.
La función es negativa cuando esta por encima del eje x.





No hay comentarios.:
Publicar un comentario